


We begin our journey in 19th-century France where Jean-Baptiste Joseph Fourier was taking part in two revolutions, one political (the French Revolution) and the other scientific (the Fourier Series), before setting off on a journey back through time to meet the mathematical giants on whose shoulders he was standing.

Arriving in 5th-century India, we meet Aryabhata, whose sine table gave us our modern day understanding of sines and cosines, the building blocks of signals. Next, we visit 16th century Italy to learn about the work of Cardano, Bombelli et al in complex number theory.

We stop by St. Petersburg Academy of Sciences in 18th century Russia to meet Leonhard Euler and discover how he combined Bombelli's rules for working with imaginary numbers with his own number (Euler's number), sines, and cosines to give us the complex exponential.

Putting all these ideas together, we learn how Fourier combined them with a weighted integration to reveal the properties of the sinusoids making up a signal, and conclude with a look at how the limitations of the Fourier Series were overcome by the work of Dirichlet et al, giving us the Fourier Transform that is so central to modern day signal analysis.

Hi, I'm Mark Newman, an electronics engineer with over 25 years of experience. I graduated from Manchester University's School of Electrical and Electronic Engineering in 1998 and have developed products ranging from robotic milking systems to devices for monitoring patients in intensive care, spending countless hours analyzing signals and implementing mathematical models. I now manage a successful YouTube channel, creating educational videos for engineering students studying signals and systems.
I believe that truly understanding the mathematical concepts behind our tools is key to unlocking their full potential. To foster that understanding, these concepts must be intuitive, with a clear grasp of their origins and the stories behind their discovery. Just as we study history to understand how the past shaped the present, learning a concept’s story reveals why it works, the problems it solves, and the insights that shaped its development.
Unsure how to use the FFT to get meaningful results from your data? In this video, I unveil 3 crucial signal preparation tips to ensure accurate frequency analysis. In this video, you'll discover:
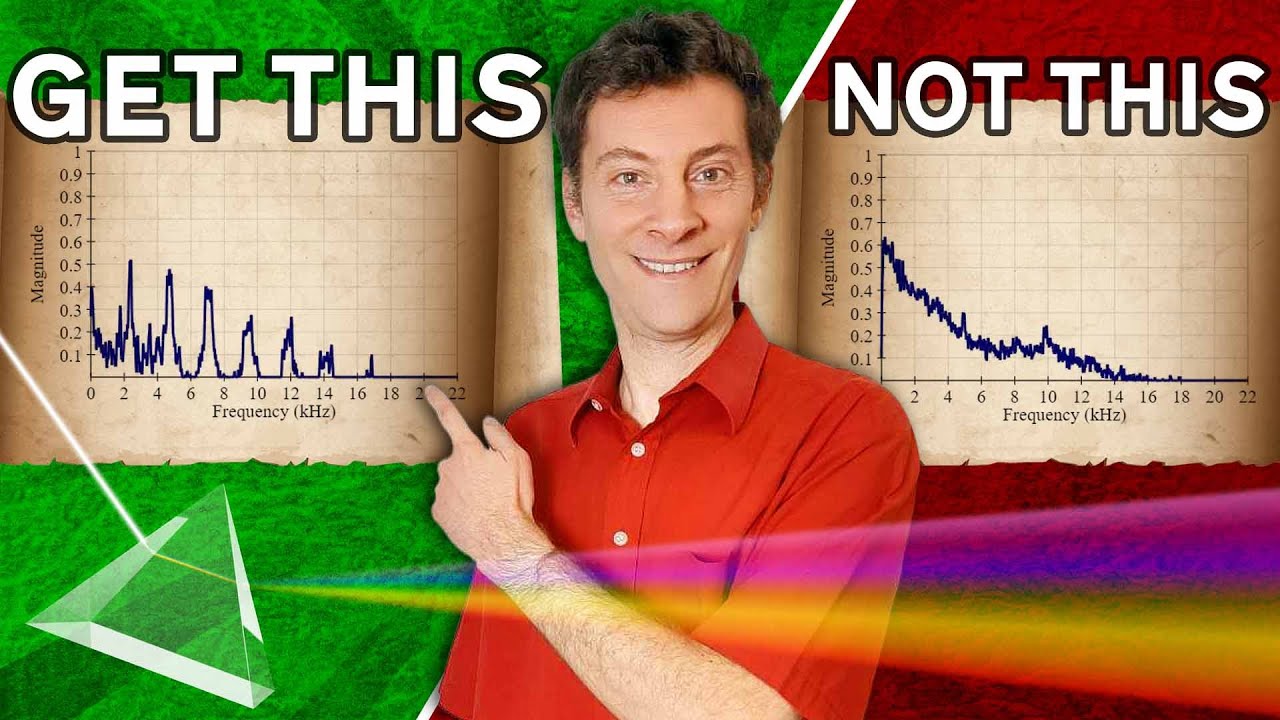

Tired of having to make sure your signal contains a specific number of samples (power of 2)? Learn how to use the FFT with signals of any length!
In this video, we’ll discover 3 powerful techniques to overcome the power of 2 limitation, discuss the pros and cons of each method, help you choose the right method for your application, and discover how to avoid data distortion and ensure accurate frequency analysis.
Baffled by the list of complex numbers the FFT gives you in its output? Don't worry, you're not alone! This video will show you how to make sense of all that gibberish.
You’ll learn how to convert the position of each item in the output list into a frequency value in Hz and find out how you can increase the resolution of your results. You'll also discover how to calculate the true strength of each frequency component in your signal and unlock the phase information to gain deeper insights into its behavior. ️

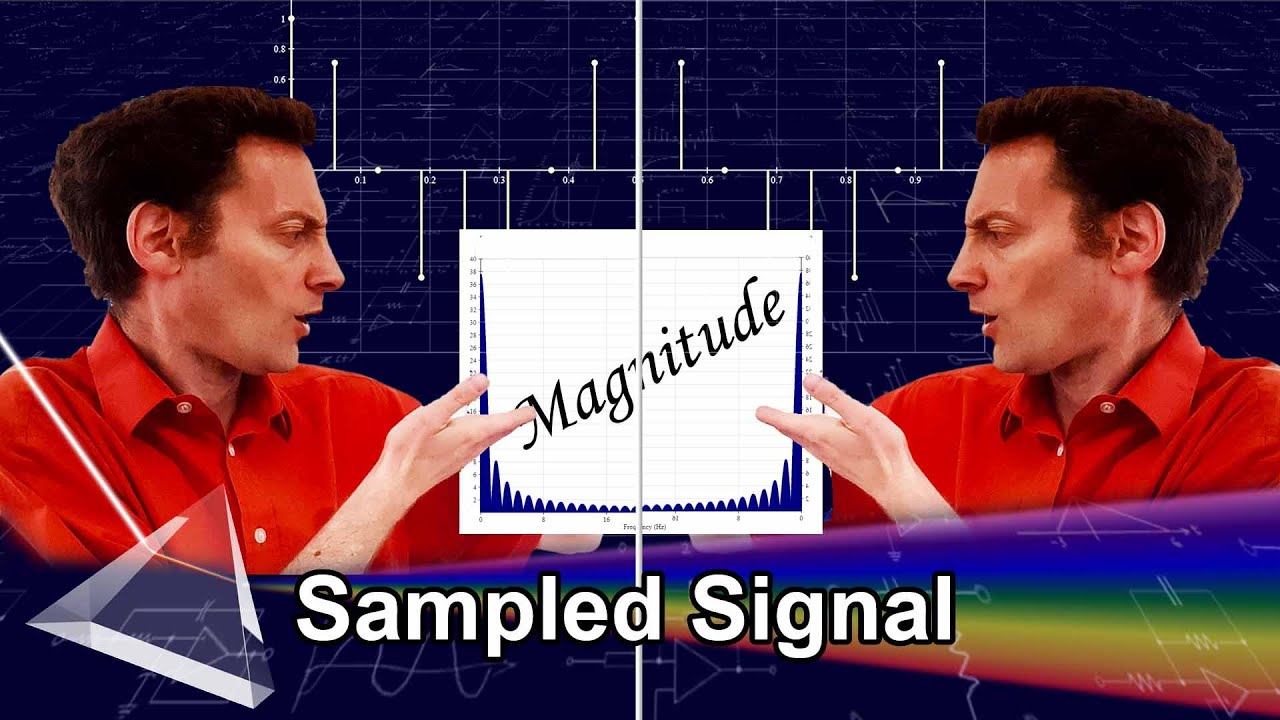
Ever wondered why the results the FFT gives you look a little bit too symmetrical? It has to do with the fact that you're signal is sampled.
In this video, I'll explain why this happens, what the Nyquist rate is, and what it means for the way you must sample your signal.
What is the format of the course?
The course is made up of a mixture of videos and worksheets, and is designed to be self-paced and accessible online. You can learn at your own convenience, where and when you want.
The videos explain each individual concept comprehensively, visually, and intuitively, and the worksheets, together with their fully worked answer sheets help you consolidate your new found knowledge by allowing you to practice each concept.
How long is the course?
The video content of the course totals just over 3 hours, (not including worksheets) spread across multiple modules. Each module includes several videos, typically ranging from 5 to 7 minutes in length, with the longest video just under 15 minutes long. The course tells the story of the Fourier Transform in episodic format, allowing you to pause, think about what you've learned, and continue when you feel ready. This episodic format makes it easier to fit the course into your busy schedule, allowing you to complete the course at your own pace.
How is the course structured?
The course is structured as a developing story, each video forming an episode of that story. As the story progresses, we introduce each of the core concepts that Fourier needed to form his theory: sine waves, complex numbers, and convolution. We look at each concept in depth, learning about its historical as well as its mathematical context.
By exploring not only the mechanics of the Fourier Transform, but also the underlying logic of the principles making it up, the course aims to equip you with a deep contextual understanding, enabling you to confidently apply its principles in many different scenarios.
Is there a prerequisite for the course?
While every effort has been made to leave no stone unturned in explaining the Fourier Transform, the course is aimed at engineers and engineering students. Therefore a basic understanding of calculus and linear algebra is an advantage. However, clear explanations and examples are provided to ensure accessibility for students from a wide range of backgrounds.
Can I access the course materials indefinitely?
Yes, once you purchase the full course, you'll have lifetime access to the course materials, including all videos and worksheets.
Can I view the course offline?
If you are using IOS, then you can download the Teachable App The app allows offline access to all courses hosted on the Teachable platform like this one.
If you are using Android, the course can only be accessed via your web browser. Therefore an internet connection is required. Unfortunately there is no Android or Desktop app currently available for the Teachable platform where this course is hosted. However, they are constantly working on new features and improvements so this answer may change in the future.
What if I don't understand something or need help on the course?
You can ask me or your fellow students questions via the course's online comments section or email me at mark@howthefouriertransformworks.com.
Do you offer a money-back guarantee?
Yes, there is a 14-day money-back guarantee. If you are not satisfied with this course within 14 days of enrollment, you are eligible for a full refund. Simply email me at mark@howthefouriertransformworks.com to request the refund.
How do I enroll in the full course?
Simply click the "See Purchasing Options" button below, choose a payment plan, and follow the on-screen instructions.